Ανδρέας Λύκος, Ματωμένο χειρόγραφο, Τραυλός, σελ. 180, 2023
Το “Έτερος εγώ” είναι από τις πιο επιτυχημένες ελληνικές ταινίες των τελευταίων πολλών χρόνων. Πράγμα που δείχνει πως, με όλη την αποστροφή προς τα μαθηματικά, που δηλώνει ένα μεγάλο μέρος του πληθυσμού, η σεναριακή αξιοποίησή τους προκαλεί μεγάλο ενδιαφέρον. Συχνά, μάλιστα, το μεγάλο ενδιαφέρον προέρχεται ακριβώς από όσους δηλώνουν αποστροφή. Ένας από τους λόγους, νομίζω, είναι το γεγονός ότι τα μαθηματικά στην αστυνομική λογοτεχνία συνδέονται πάντα με διανοητικά ερεθιστικούς γρίφους -πράγμα που, ίσως, κάτι θα έπρεπε να λέει και για τις διδακτικές των μαθηματικών.
Στο “Έτερος εγώ” η ιδέα πάνω στην οποία στηρίζεται η ιχνηλάτηση των βημάτων του κατά συρροήν δολοφόνου είναι οι φίλιοι αριθμοί, οι οποίοι ορίζονται ως εκείνοι για τους οποίους το άθροισμα των γνήσιων διαιρετών του ενός είναι ο άλλος και το αντίθετο.
Τι ἐστί φίλος; Έτερος ἐγώ.
Φίλος είναι ο άλλος μου εαυτός. Φίλιοι είναι οι αριθμοί, που καθρεφτίζεται ο ένας μέσα στον άλλο. Δεδομένου ότι οι διαιρέτες είναι σημαντικότατοι αριθμοί, μπορούν να κατοχυρώσουν και την αριθμητική φιλία.
Οι αριθμοί 220 και 284, γι’ αυτό το λόγο, για τους Πυθαγόρειους ήταν σύμβολο φιλίας. Ας το δούμε αναλυτικά.
Οι γνήσιοι διαιρέτες του 220 είναι οι αριθμοί 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110. Αν τους προσθέσουμε διαπιστώνουμε ότι το άθροισμα είναι 284.
Αντίστοιχα, οι γνήσιοι διαιρέτες του 284 είναι οι 1, 2, 4, 71, 142, με άθροισμα 220.
Η ταινία εκτυλίσσεται αξιοποιώντας σεναριακά τους αριθμούς αυτούς, πράγμα που της δίνει το ιδιαίτερο ενδιαφέρον της.
Σε άλλη περίπτωση έχουν χρησιμοποιηθεί οι τέλειοι αριθμοί, αυτοί, δηλαδή των οποίων το άθροισμα των γνήσιων διαιρετών είναι ο ίδιος ο αριθμός.
Δείτε, π.χ., τον 6. Γνήσιοι διαιρέτες του είναι οι αριθμοί 1, 2 και 3. Προσθέτοντάς τους παίρνουμε άθροισμα 1+2+3 =6. Επόμενος τέλειος είναι ο 28, όπως εύκολα μπορείτε να διαπιστώσετε (1+2+4+7+14 =28). Μετά έρχεται ο 496 και στη συνέχεια ο 8128. Και γι’ αυτούς η επαλήθευση είναι περισσότερο απαιτητική υπολογιστικά, αλλά εύκολη και πάλι. Αυτοί ήταν οι μόνοι γνωστοί τέλειοι για τους αρχαίους Έλληνες.
Πράγμα λογικό αν σκεφτείτε ότι ο επόμενος τέλειος αριθμός είναι ο 33.550.336, ο μεθεπόμενος 8.589.869.056, ενώ ο ένατος στη σειρά είναι ο εκπληκτικός αριθμός 191.561.942.608.236.107.294.793.378.084.303.638.130.997.321.548.169.216. Και έπεται συνέχεια!
Ο ειδικός σε αυτές τις ιστορίες επιχειρεί και σχεδόν, αλλά όχι πάντα, κατορθώνει να συνδέσει τη σειρά των εγκλημάτων με τις ιδιότητες αντίστοιχων αριθμών. Ο δολοφόνος είναι συχνά εξίσου ικανός στα μαθηματικά με τον μαθηματικό βοηθό του ντετέκτιβ. Πράγμα που δίνει ένα βάθος στην ιστορία και προκαλεί διαρκώς το ενδιαφέρον.
Στην περίπτωση του “Ματωμένου χειρόγραφου”, ο Ανδρέας Λύκος χτίζει την ιστορία του γύρω από το περίφημο Παλίμψηστο του Αρχιμήδη, του μεγαλύτερου, ίσως, μαθηματικού όλων των εποχών -αν έχει νόημα να μιλάμε για τον ένα «μεγαλύτερο».
Ο ειδικός στην Ιστορία των Μαθηματικών Αριστοτέλης Γαλάνης θα εμπλακεί, μαζί με τον αστυνόμο Γιάννη Λόντσα, στη διερεύνηση μιας σειράς φόνων, που συνδέονται με τη δημοπράτηση ενός μεσαιωνικού χειρογράφου, αντιγράφου του Παλίμψηστου. Όλοι όσοι, από μεριάς του ελληνικού κράτους και του Υπουργείου Πολιτισμού, εμπλέχτηκαν στην αποτυχημένη διεκδίκησή του το 1999 στον οίκο Christie’s της Νέας Υόρκης έγιναν στόχοι δολοφονικών ενεργειών πέντε χρόνια μετά, τη χρονιά των Ολυμπιακών της Αθήνας. Ο δολοφόνος αφήνει στους τόπους του εγκλήματος μια σειρά από γεωμετρικά σχήματα, τρίγωνα, τετράπλευρα και πεντάπλευρο. Ο αριθμός των σχημάτων ακολουθεί τη σειρά 2, 4 και 8. Σε κάθε ένα από αυτά υπάρχουν γράμματα τα οποία, όμως, δεν βγάζουν νόημα ούτε μερικά ούτε ως σύνολο.
Ο Γαλάνης θα πρέπει να βρει τι σημαίνουν όλα αυτά. Πρόκειται για την ακολουθία αριθμών 2, 2*2= 4, 2*4 =8, …; Την ακολουθία, δηλαδή, όπου ο κάθε όρος είναι διπλάσιος του προηγούμενου; Που σημαίνει πως οι αριθμοί που ακολουθούν θα είναι 16, 32, 64, 128,…;
Πιθανόν. Όχι, όμως, βέβαιο, αφού αυτή η τριάδα αριθμών, μπορεί να ανήκει και στην ακολουθία 2, 4, 8, 16, 31. Όπου οι αριθμοί δείχνουν τις περιοχές στις οποίες χωρίζεται ένας κύκλος αν ενώσουμε δύο σημεία της περιφέρειας του, στη συνέχεια τρία σημεία, μετά τέσσερα, πέντε, έξι. Στην τελευταία περίπτωση, διαπιστώνουμε, όπως φαίνεται στο σχήμα ότι οι περιοχές, που προκύπτουν είναι πράγματι 31 -και όχι 32!
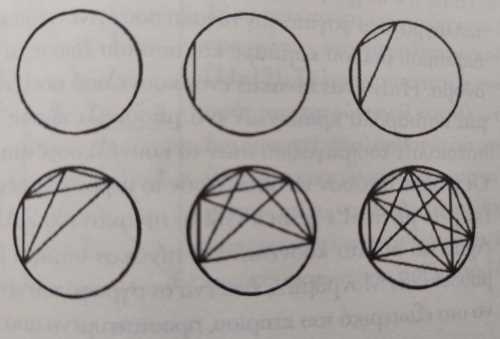
Ή σημαίνει κάτι το άθροισμα των αριθμών 2+4+8 =14; Μήπως τα 14 σχήματα που βρέθηκαν στους τόπους των εγκλημάτων συνδυάζονται με τρόπους που οδηγούν στην αποκωδικοποίηση των γραμμάτων που βρίσκονται χαραγμένα πάνω τους φτιάχνοντας κανονικά, δηλαδή ισόπλευρα σχήματα;
Και αν το 2 αντιστοιχεί σε εκατοντάδες, το 4 σε δεκάδες και το 8 σε μονάδες, άρα όλοι μαζί παραπέμπουν στον αριθμό 248;
Το βιβλίο του Λύκου χειρίζεται αυτό το υλικό με πολύ ενδιαφέροντα τρόπο και είναι εξαιρετικά λιτό -τίποτε στην ιστορία, που μας λέει, δεν περισσεύει. Συνδέει την ιστορία του με υπαρξιακά, καθημερινά, δηλαδή, στοιχεία της ζωής των ηρώων – πλήξη, φόβο, ενοχές, αλλά και αγάπη. Όλα χαμηλότονα, τίποτε ιδιαίτερα δραματικό, όπως είναι συνήθως η ζωή μας.
Δίνει, μάλιστα, και μια, όχι κυρίαρχη, αλλά πάντως σημαντική πολιτική χροιά στα γεγονότα. Χωρίς, όμως, να τοποθετείται με κραυγαλέο τρόπο μετατρέποντας τη λογοτεχνία σε όχημα με άλλες στοχεύσεις. Δεν θέλει να γράψει δοκίμιο, αλλά μυθιστόρημα. Και μας δίνει μια αξιοσημείωτη δυνατότητα να «χαθούμε» στις ιστορίες και μαζί, ίσως, να αγαπήσουμε τα μαθηματικά.



